モーダルサーベイ試験

モーダルサーベイ試験は、試験する物体に対して低レベルでの加速度を振動試験機で負荷させ、得られ加速度応答データから物体の固有値周波数(振動数)や物体の振動による変形(振動モード)を得る試験のことをいいます。全機振動試験/共振点探査/振動応答検査ともいわれます。
試験自体はランダム振動試験や正弦波振動試験の低加速度レベルで試験されます。
- モーダルサーベイ試験
- モーダルサーベイ試験と宇宙機開発の関係
- モーダルサーベイ試験の取得周波数範囲
- 宇宙機でのモーダルサーベイ試験のデータ取得の目的
- モーダルサーベイ試験は正弦波振動試験かランダム振動試験か
- 共振点探査の共振とモード解析
- 設計初期段階での構造シミュレーションの大切さ
- ハンマリング法
- モーダルサーベイ試験は正弦波振動とランダム振動のどっちでやるの?
- 振動試験で主に得られるデータ
モーダルサーベイ試験と宇宙機開発の関係
モーダルサーベイ試験は、宇宙機の機械環境試験でもよく使用されています。
一つは、ロケットの打上げ振動、あるいはモーターを含む駆動部品、製品内部の部品同士が共振する周波数(共振周波数)にないことを確認するために試験を実施します。
さらには、ロケットの打上げ環境を模擬した高負荷を掛けるランダム振動試験や正弦波振動試験などの振動試験前後で行われ、高負荷を掛けた振動試験中に、構造的な破損が発生していないかを確認する際に使用されます。
物体の固有値周波数や振動モードのデータを得ることにより、物体を分解せずとも物体内部(電子部品や基板、ネジなど)の破損の有無を推定することを可能としています。
また、目視では確認できない構造的な異常の有無をデータにより確認する方法としても利用されます。
ただしこの使われ方は一般的ではなく、通常の製品でモーダルサーベイ試験を実施する場合は、試験体の共振周波数を取得することをメインとしており、物体の破損の確認のために主要な負荷をかける振動試験前後の2回で実施されることはとても少なく、試験前の一回で終わることが多いようです。
一般的には、内部部品同士や搭載先の部品との共振が発生していないかを確認しつつ、構造シミュレーション結果とモーダルサーベイ試験の結果を合わせることにより、構造シミュレーションで構築する数学モデルの精度を向上させることにも使用されます。
モーダルサーベイ試験の取得周波数範囲
人工衛星の場合、モーダルサーベイ試験の取得周波数帯は20-2000Hzと広域で取得されることが多いです。
一方、通常の製品の場合はそこまでの広域を取得することは少なく、200Hzまでであったり、500Hzまでであることが多いです。
これは、どの加振機であっても、高周波数帯でノイズを受けてしまい、精度が低くなってしまうことが理由となります。
精度が低いのであれば、取得する必要性も低下します。
特に正弦波振動でのモーダルサーベイ試験は、取得周波数帯がそのまま試験時間に直結してしまうため、短い範囲で取得した方が費用的にも安くなります。
人工衛星を含めた宇宙機の場合は、前述のように振動試験による故障を分解せずに推定する、さらにいうと試験対象の組み立ての確からしさ(ワークマンシップ)を確認することも目的の一つにしています。
そのため、(高周波数帯を含めた)広域の周波数帯のデータを取得した方が得られるデータが多く、実際に不具合が発生したときに有利に働くことが往々にしてあります。
宇宙機では、試験回数も多量に生産しないため試験用の製品でも高価で、複数台作られることが少なく、また、披露蓄積の観点から複数回試験することも少なく、試験そのものが貴重な機会になります。
このように広域で取得された周波数帯のうち、低周波数帯は外部(ロケットなど)の固有値振動数と共振しないかを確認するためであり、高周波数帯は前述のとおり物体の構造的な異常を確認しています。
一方で高周波数帯のデータは、高速フーリエ変換(FFT)を使用してもノイズが大きく、宇宙機を試験したことのない振動試験作業者からは意味のないように思われることも多くみられるのは事実です。
しかし高周波数帯のブロードな形状は、構造物全体の傾向や試験前後の異常を検知するための判断要素になりえます。
宇宙機でのモーダルサーベイ試験のデータ取得の目的
宇宙機でのモーダルサーベイ試験のデータ取得は、共振周波数を確認することを目的の一つにしているのですが、宇宙機の場合は優先度としては低めに設定されます。
というのも、宇宙機の場合は打ち上げない試験用で打ち上げる機体とほぼ同一の構造を持つEM(エンジニアリングモデル)、あるいはSM(ストラクチャーモデル)を利用して、事前に確認していることが多いのが理由です。
ちなみに一部の宇宙機の開発プロジェクトでは、EMあるいはSMを製造しない選択肢を取っていることもあります。これはリスクを検討した上での選択しています。
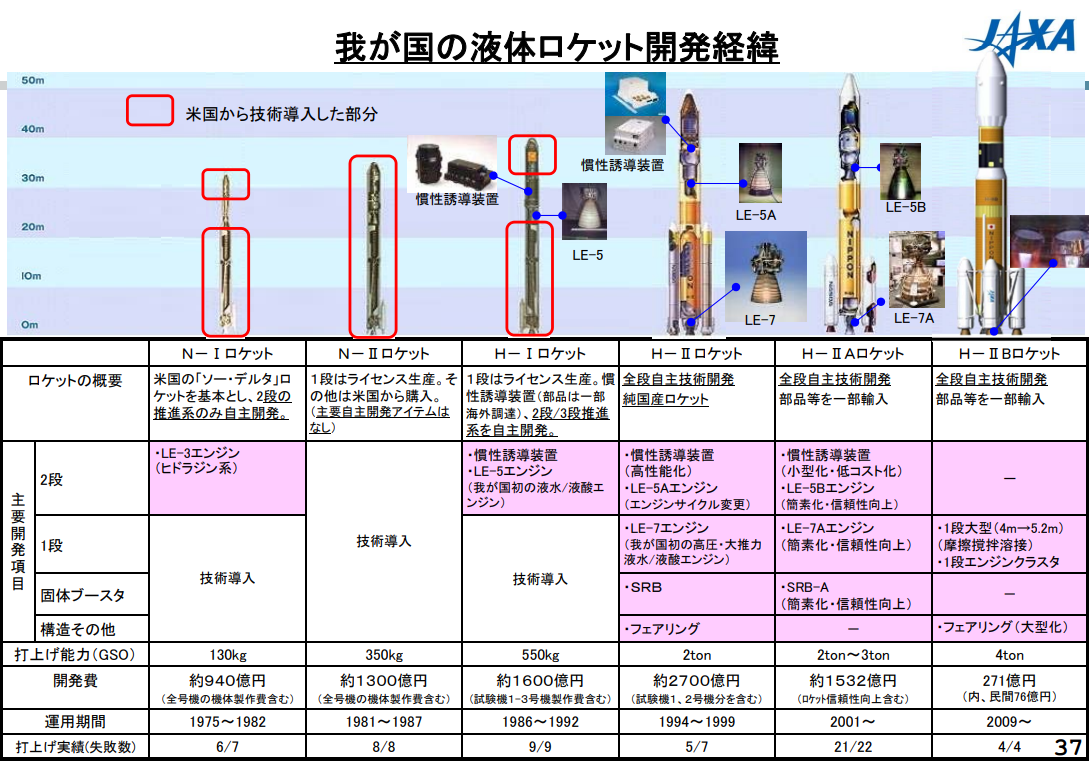
この辺りは特に、特定の開発手法というものはなく、各開発プロジェクトの様々な事情から選択されます。
開発上の確実性を狙うのであれば、いくつかのモデルを製作するべきですが、資金やスケジュールの問題からしばしばすべてのモデルを製造することが難しくなっています。
頭ごなしに開発手法を否定せず、リスクや制限条件を明確にしたうえで、実施の有無の判断をしていきましょう。
例えば、やり直しをリカバーできるだけのスケジュール感、過去と類似設計であるために、構造的には問題ないという判断、精度の高い構造シミュレーションモデルの製作ノウハウなどがその一端にはなりえます。
省略する場合は、何を犠牲にしてプロジェクトを進めているのか認識し、話し合った上で進めることをお勧めします。
プロジェクトは後になればなるほど、被害やストレスが過大になっていくものです。
モーダルサーベイ試験は正弦波振動試験かランダム振動試験か
モーダルサーベイ試験としては正弦波振動試験とランダム振動試験を使用します。
正弦波振動試験は、周波数をスイープして加振させていくために、特定の周波数帯で大きく振幅すれば、固有値振動数や共振が起きていると感覚的にも理解できるのではないでしょうか。
ではランダム振動試験が利用されているのはなぜでしょうか。
ランダム振動にはその名の通りランダムな振動要素が含まれており、その中に正弦波振動の成分もあります。
そのため、ランダム振動試験の条件でのモーダルサーベイ試験を実施しても共振点を探ることができます。
ランダム振動は正弦波振動以外にも複数の振動が組み合わされており、比較的実際の環境に近い振動環境を負荷させることができます。
モーダルサーベイ試験における正弦波振動試験やランダム振動試験は、製品の機能性能を確認する試験ではありません。
加速度も1Gにする必要もなく、掃引速度もあまりにゆっくりである必要もありません。
宇宙機では正弦波振動試験で実施する場合、掃引速度が4oct/min程度でも取得することが多いです。
一般製品の場合は、JIS規格(JIS C 60068-2-64:2011 (IEC 60068-2-64:2008) 、振動応答検査の欄)で1oct/min以下とされていることから、1oct/minを設定するプロジェクトが多い気がします。
共振点探査の共振とモード解析
共振は物体の固有値振動数(周波数)と外部の振動数(周波数)が一致した状態をいいます。
共振になると、減衰(ζ)がなければ周波数の振幅が無限大に増大していきます。
実際の構造は減衰が存在するために、振幅が無限大になることはありません。
この振幅の倍率は共振倍率Q=1/(2ζ)で計算され、どれだけ振幅が増幅するかを示しています。この計算式でわかる通り、振幅の増幅は物体の減衰によって計算されます。
振幅が大きくなると、物体が大きく震える(揺れる)ため、変形を引き起こし、物体の強度を越えると破壊されてしまいます。
振幅の大きさ(単位:m)と、振幅が1秒間に何回振動するか(振幅の波が何回発生するか)は振動数(単位:Hz)によって表されます。
複数の物体の振動数が、同じあるいは近いと振動が合成され、振幅が大きくなっていき、いわるゆる共振を発生させます。
構造設計では、固有振動数(物体が持つ固有の共振周波数】を構造シミュレーションや実試験により算出します。
物体の固有値振動数(周波数)と内外部からの振動による振動数(周波数)を離すために、部分的な物体の剛性を高くするなどの設計することが重要な課題となります。
文頭にざっくり述べましたがモーダルサーベイは、物体の構造を理解するための手法です。共振点探査や振動応答検査とも称されます。振動応答検査はJIS内で記述があるのですが、業界や組織によって呼称はまちまちであることも注意が必要です。
物体は、ある周波数で励起される(外部から特定の周波数を受ける)と、モードと呼ばれる特定の形状で振動あるいは変形します。この振動や変形も、複雑な組み合わせにより様々なモード形状が発生します。
試験や解析により、構造の固有値振動、モード減衰、およびモード形状を特定することをモード解析と呼ばれることもあります。
試験以外でもモード形状と固有振動数は、有限要素解析モデルといわれる数学的モデルを使用して予測することができます。構造シミュレーションや構造解析といわれます。
固有値振動数を確認し、共振周波数の情報を入手することで、物体がどの周波数帯域で振動するかを知ることができ、モード解析により、どのような変形をするのか知ることができます。
さらに変形量や物体への負荷を知るには、物体に対して外部からどのような負荷が掛かるのか、振動試験条件による負荷から算出することができます。
この負荷はマイルズの式により算出することができます。
mechanical-systems-sharing-ph.hatenablog.com
設計初期段階での構造シミュレーションの大切さ
構造シミュレーションはエンジニアが構造物を設計した時に、実物を製造する前に構造特性を理解するのに役立ちます。近年ではバーチャルエンジニアリングとも呼ばれる手法の一端を成しています。
この数学モデルも、設計の初期段階や初めて解析をする場合などは、実際に製造した構造物と差異があるため、ある程度の精度を得るまでは、試験機などを利用して実際もモーダルサーベイ試験結果と照合していくことで、物体の構造特性を理解する助けになります。
構造シミュレーションの経験者は、設計段階の不確かな部分を考慮しつつ、実際に製造した構造物と数学モデルで再現できない部分を考えながら、製品の評価をしていくことがとても大事です。
例えば、全ても固有値振動数を数%単位で合わせこむことは初期段階やある程度の製品の振動特性情報の蓄積がないと厳しい。
設計者が欲している都合の良い結果が出ることは少ないため、多面的な視点が必要になります。
特に初期から構造シミュレーションを取り入れずに、問題が発生してから取り入れる場合は、時間的制約や製造的な制約も発生するため、解析した結果を精査することが難しくなってしまうこともあります。
その場合は実際の製造物の固有値振動数などの振動特性をの合わせこみは止めて、振動特性の傾向に絞り込むのも一つの手段です。
どのモードが低周波数帯で発生するのか、最も揺れるモードがどこにあるのかなどを探っていくというのも分析手法としてはありです。
これらの確認は、設計の早いフェーズで実施していた方が、設計・製造の出戻りが少ないです。
宇宙機のコンポーネントでいうと、電子部品がたくさん載っている基板の揺れを抑え込むために、支柱を増やしたり、座金の径を大きくしたり、ねじのサイズを上げたり、ねじの本数を上げたり、いくつかの材料を変更したり、振動を低減させるダンパーのようなものを追加するなどの具体的な案を取りやすくなります。
これらは設計後半になるほど、基盤の部品密度が高くなりすぎて、重量部品の移動ができなかったり、放熱のためのヒートシンクの場所や大きさが限定されてしまうことにより、設計・開発者を非常に悩ませます。
宇宙機のコンポーネントの場合は削り出しであることが多く、再製作や再加工に時間がかかってしまうことが予想されます。
ハンマリング法
モーダルサーベイ試験には、ハンマリングと呼ばれるインパクトハンマーによる方法とモーダルシェイカーという方法が一般的です。
モーダルシェイカーとは、簡単に言い過ぎると振動加振機上で実際に筐体を振動させることです。小型もあります。
モーダルシェルカーが使われる理由の一つは、ハンマリングの方が筐体に対して何度も不均一な衝撃を加えるため、ダメージが予想できにくいことと、数メートルクラスの宇宙機に対して適度な威力で振動させることが難しいためです。
もしかすると、衝撃試験機により均一な衝撃を与えることが可能になっているかもしれませんが。
さて、数メートルクラスの宇宙機に対して衝撃を与えるほどのハンマリングの装置を準備するよりも、振動試験機(加振機)を使用した方が安定しており、すぐに振動試験に移行できるために時間的にも有利で、比較的再現性が高いということも理由の一つです。
モーダルサーベイ試験は正弦波振動とランダム振動のどっちでやるの?
モーダルサーベイ試験は前述のとおり、正弦波振動とランダム振動の両方で目的の振動特性を取得することができます。
そして、比較的ランダム振動で取得することが経験的には多いです。
というのも、正弦波振動試験の方がランダム応答試験よりも試験対象に付加される構造的なストレスが大きいためです。
感覚的には逆に思われる人が多くいそうですが、共振探査ではない正弦波振動試験も、ランダム振動試験よりも強い負荷を掛けられることが多いです。
実際にランダム振動試験より正弦波振動試験の方が、物理的な損傷による不具合が多くはないでしょうか? (これは経験則に寄るかもしれませんが)
このような理由から、宇宙機への負荷を減らしたいためにランダム振動試験を選択するプロジェクトが多くなっているのではないでかね。
もちろんランダム振動試験にもデメリットがあり、ランダム振動を負荷されていることから、想定とは違う回数のストレスを宇宙機に負荷されてしまいます。
おそらくは負荷の回数よりも宇宙機自体の負荷(ダメージ)を選択した結果でランダム振動を負荷させているのではないかと思います。
ただ、固有値振動数、共振周波数の正確性の確認を主としつつ、ある程度ダメージを得ってもよいモデル(試験用試作品)の場合は、正弦波振動試験の方が比較的正確性が高いです。
この辺りはプロジェクトの考え方次第です。
振動試験で主に得られるデータ
振動試験で主に得られるデータは、周波数応答関数(FRF)、コヒーレンスの信号データを注目します。
これらの信号による線形スペクトルから、パワースペクトルやクロスパワースペクトルを計算します。測定値はノイズも多いため、高速フーリエ変換を用いて平均化していきます。
周波数応答関数は、加振させる入力信号と加振により反応した出力信号の2つの信号から計算されます。伝達関数ともいわれます。
一般に出されるスペクトルはこの周波数応答関数によるものです。取得データの分解能が低い(取得データの周波数単位が少ない)場合は、高速フーリエ変換をしてもギザギザと荒い形状を成すことが多いです。
コヒーレントは周波数応答関数に関係して、加振により反応した部分が励起に起因するかを示し、測定自体の評価に使用されます。
縦軸が0から1で示され、基本は1側に張り付いており、構造的な応答が悪い場合に低くなる傾向があります。
参考文献
JIS C 60068-2-64:2011 (IEC 60068-2-64:2008) 環境試験方法−電気・電子− 第2-64部:広帯域ランダム振動試験方法及び指針
https://kikakurui.com/c60/C60068-2-64-2011-01.html
Basics of Modal Testing and Analysis
https://www.crystalinstruments.com/basics-of-modal-testing-and-analysis
設計において共振周波数を改善する方法とは?
https://d-monoweb.com/blog/improve-resonance-frequency/
周波数応答解析
https://www.fem-vandv.net/c27.html
第 4 章 環境試験・検証試験
https://kitsat.net/documents/Nishimura_part1_4.pdf
大型衛星に対する振動試験
https://www.jstage.jst.go.jp/article/jjsass1969/31/355/31_355_428/_pdf/-char/ja










![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1cd3468d.0c08f3fc.1cd3468e.10b04370/?me_id=1213310&item_id=20370886&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F9208%2F9784339029208_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext)